Քվանտային համակարգիչներ, քվանտային կրիպտոգրաֆիա, քվանտային հաշվարկ․ տեխնոլոգիաներ ապագայի՞ց, ներկայի՞ց, թե՞ չբացահայտված կախարդանք

Իսկ ի՞նչ է ընդհանրապես քվանտային մեխանիկան, և ինչպե՞ս է այն առաջ եկել։ 20-րդ դարում ֆիզիկոսները համարում էին, որ նրանք կարողացել են բացատրել բոլոր երևույթները և ստեղծել են ամբողջական ու կատարյալ տեսություն։ 1900 թ. լորդ Կելվինը իր դասախոսություններից մեկի ժամանակ ասել է, որ ֆիզիկայում նոր բան չկա հայտնաբերելու, մնում է միայն ավելի ու ավելի ճշգրիտ չափումներ կատարել: Սակայն կարճ ժամանակ անց գիտնականները բախվեցին բազմաթիվ խնդիրների, որոնք չէին բացատրվում դասական ֆիզիկայի տեսությամբ։ Դրանցից են, օրինակ, սև մարմնի ճառագայթումը և ֆոտոէֆեկտը, որոնցում ի հայտ եկած լույսի հատկությունները հնարավոր չէր բացատրել էլեկտրամագնիսական դաշտի մաքսվելյան տեսության օրենքներով։ 

Այնուհետև էլեկտրոնի հայտնագործումից և ատոմի կառուցվածքի ուսումնասիրություններից առաջացան նոր խնդիրներ։ Ռեզերֆորդի փորձերից (առավել մանրամասն՝ այստեղ) հայտնի դարձավ, որ ատոմն ունի համեմատաբար շատ մեծ զանգված, փոքր չափեր ունեցող դրականապես լիցքավորված միջուկ և դրա շուրջը պտտվող էլեկտրոններ` լիցքավորված բացասականապես։ Ըստ դասական էլեկտրադինամիկայի՝ արագացումով շարժվող լիցքավորված մասնիկը ճառագայթում է էլեկտրամագնիսական ալիքներ, և որոշ ժամանակ անց էլեկտրոնները, ճառագայթման արդյունքում իրենց էներգիան կորցնելով, պիտի ընկնեին միջուկի վրա։ Բայց, ինչպես գիտենք, սա տեղի չի ունենում, հակառակ դեպքում` բնության մեջ կայուն ատոմներ գոյություն չէին ունենա։ 

Դեռևս 19-րդ դարի սկզբին Թոմաս Յունգն ու Օգյուստեն Ֆրենելին հայտնագործել են լույսի ալիքային բնույթը` ինտերֆերենցի և դիֆրակցիայի (այս երևույթներին առավել մանրամասն հնարավոր է ծանոթանալ այստեղ) փորձերի միջոցով։ 20-րդ դարի սկզբին առաջ քաշվեց էլեկտրամագնիսական ալիքների երկակի բնույթի գաղափարը, ըստ որի, լույսը որոշ դեպքերում դրսևորում է ալիքային, որոշ դեպքերում` մասնիկային հատկություններ։ 

Լուի դը Բրոյլը 1924 թ. առաջ քաշեց մի վարկած, ըստ որի, նույն ձևով, ինչպես ֆոտոնները, նյութի մասնիկներն էլ պիտի օժտված լինեն ալիքներին բնորոշ հատկություններով` յուրաքանչյուր շարժվող մասնիկ ունենա իրեն համապատասխան ալիք, որը կոչվում է Դը Բրոյլի ալիք։ Կախված արտաքին պայմաններից՝ միկրոմասնիկը դրսևորում է իր մասնիկային կամ ալիքային հատկությունները։ Այսպիսով, պարզվեց, որ դասական ֆիզիկայի օրենքները չեն գործում ատոմական աշխարհում։ Միկրոաշխարհի օրինաչափություններն ուսումնասիրող տեսությունն անվանվեց քվանտային մեխանիկա։ Քվանտային մեխանիկան սահմանային դեպքում հանգում է դասական մեխանիկային։

Ալիքային ֆունկցիա

Դասական ֆիզիկայում մարմնի դիրքը տվյալ պահին կարող ենք նկարագրել` տալով նրա կոորդինատները և իմպուլսները։ Եթե այսպիսի ձևով նկարագրեինք տարրական մասնիկների դիրքերը, կնշանակեր, որ նրանք ունեն շարժման որոշակի հետագիծ և դասական մասնիկներ են։ Այս դեպքում չէինք կարողանա հասկանալ, թե ինչպես են տեղի ունենում, օրինակ, էլեկտրոնների դիֆրակցիայի և ինտերֆերենցի երևույթները։ Այսինքն, պետք է ներմուծենք մի ֆունկցիա, որը կտա մասնիկի վիճակի բնութագիրը։ Այն կոչվում է ալիքային ֆունկցիա։ Բայց ի՞նչ է ալիքային ֆունկցիան և ի՞նչ կտա մեզ, եթե այն գտնենք։ Վերջիվերջո, մասնիկը գտնվում է տարածության որևէ կետում, իսկ ալիքային ֆունկցիան բաշխված է տարածության մեջ, ինչպե՞ս կարող է այն նկարագրել մասնիկի դիրքը։ Ըստ Բոռնի տեսության՝ ալիքային ֆունկցիայի մոդուլի քառակուսին ցույց է տալիս հավանականության խտությունը, որ մասնիկը կգտնվի կոորդիտաների  x,x+dx, y,y+dy, z,z+dz միջակայքում ժամանակի t պահին։ Սա քվանտային մեխանիկայի մեջ մտցնում է ինդետերմինիզմի գաղափարը` երևույթները չունեն օրինաչափ բնույթ, այլ տեղի են ունենում պատահականորեն։ Այսինքն, անգամ եթե մենք ունենք մասնիկը նկարագրող ալիքային ֆունկցիան, մենք չենք կարող հստակորեն որոշել նրա դիրքը հաջորդ պահին։ Սա բազմաթիվ դժվարություններ է առաջացրել ֆիզիկոսների շրջանում․ արդյո՞ք սա ուղղակի բնության աշխատանքի մեխանիզմն է, թե՞ տեսության ոչ ամբողջական լինելը։

Ենթադրենք՝ մենք չափեցինք մասնիկի դիրքը և գտանք նրան  A կետում։ Հարց է առաջանում, թե որտե՞ղ էր մասնիկը անմիջապես չափումից առաջ։ Կան այս հարցին պատասխանող 3 տարբեր տեսակետներ․

1. Ըստ ռեալիստների՝ մասնիկը գտնվում էր հենց A կետում։ Եթե անգամ սա ճիշտ պատասխան է, քվանտային մեխանիկան ոչ ամբողջական տեսություն է, քանի որ չի կարողանում բացատրել, թե ինչո՞ւ էր մասնիկը հենց այդ կետում։ Ռեալիստների համար ինդետերմինիզմը ոչ թե բնության աշխատանքի մեխանիզմն է, այլ որոշ փաստերի՝ մեր կողմից չբացահայտված լինելու պատճառը։ Ստացվում է, որ մասնիկի դիրքը երբեք անորոշ չի եղել, այլ պարզապես անհայտ է եղել փորձարարին։

2. Ըստ մյուս տեսակետի՝ մասնիկն իրականում ոչ մի տեղ էլ չէր գտնվում, մեր չափման հետևանքն էր, որ ստիպեց նրան հայտնվել որևէ կետում։ Այսինքն՝ չափումները ոչ միայն ազդում են մասնիկի դիրքի վրա, այլև ստեղծում են այդ դիրքը։ Այս դիրքորոշումը անվանում են կոպենհագենյան ինտերպրետացիա։ Ֆիզիկոսների շրջանում սա ամենատարածված տեսակետն է։ Եթե այս տեսակետն է ճիշտ, ապա մեր չափումների մեջ ինչ-որ անսովոր և տարօրինակ բան կա, որը արդեն մեկ դար է՝ անհայտ է գիտնականներին։

3. Ըստ ագնոստիցիզմի հետևորդների՝ այս հարցն իրականում պատասխան չունի։ Ի՞նչ իմաստ կա ենթադրություններ անել մասնիկի դիրքի վերաբերյալ մինչ չափումը, եթե ենթադրության ճշտությունն իմանալու միակ ձևը հենց չափում անելն է։ Սա մետաֆիզիկա է. մտածել բաների մասին, որոնք բնականորեն չեն կարող փորձարկվել, ինչպես, օրինակ, ժամանակը, տարածությունը և այլն։

Մինչև վերջերս այս 3 տեսակետներն էլ ունեին իրենց հետևորդները, բայց  1964 թ. Ջոն Բելը ցույց տվեց, որ մեծ տարբերություն կա նրա մեջ, թե մասնիկն ուներ հստակ դիրք, որն անորոշ էր մեզ համար, թե չուներ։ Սա ցույց տվեց, որ վերջին տեսակետը սխալ և անիմաստ է։ Մնում էր փորձերի միջոցով հասկանալ առաջին կամ երկրորդ տեսակետի ճշտությունը։ Փորձերը հաստատեցին  երկրորդ մեկնաբանությունը. մասնիկը պարզապես չունի ճշգրիտ դիրք մինչև չափումը:

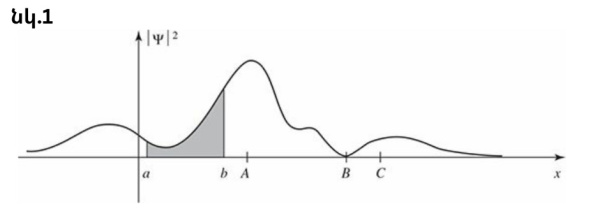
Իսկ ի՞նչ կլինի, եթե անմիջապես կատարենք երկրորդ չափումը։ Արդյո՞ք մասնիկը կգտնվի A կետում, թե՞ ցանկացած չափում ամեն անգամ տալիս է լրիվ նոր արդյունք։ Այս հարցն արդեն ունի հստակ պատասխան` կրկնված չափումը նույն մասնիկի վրա վերադարձնում է նույն արդյունքը։ Իրոք, դժվար կլիներ ապացուցել, որ մասնիկը իսկապես գտնվել է A կետում առաջին դեպքում, եթե դա չհաստատվեր չափման կրկնությամբ: Ինչպե՞ս է այս մեկնաբանությունը բացատրում այն ​​փաստը, որ երկրորդ չափումը պետք է տա ​​նույն արժեքը: Առաջին չափումը լրիվ փոխում է ալիքային ֆունկցիան, այնպես որ այն կտրուկ մաքսիմում է ունենում A կետի մոտ (տե՛ս նկ. 1) (ալիքային ֆունկցիան կոլապսի է ենթարկվում): Ըստ Շրյոդինգերի հավասարման (որի մասին կկարդաք մի փոքր անց)՝ ֆունկցիան նորից վերադառնում է իր դիրքին, ուստի երկրորդ չափումը պետք է կատարվի շատ արագ։  

Քվանտային սուպերպոզիցիա

Քվանտային սուպերպոզիցիան քվանտային մեխանիկայի հիմնարար սկզբունք է, որը հնարավորություն է տալիս մասնիկին կամ քվանտային համակարգին միաժամանակ գոյություն ունենալու մի քանի վիճակներում։ Այս երևույթը քվանտային և դասական աշխարհների ամենակարևոր տարբերություններից մեկն է: Դասական աշխարհում օբյեկտը տվյալ պահին կարող է գտնվել միայն մեկ վիճակում:

Սուպերպոզիցիայի գաղափարը հասկանալու համար եկե՛ք պատկերացնենք մետաղադրամ, որը պտտվում է օդում: Երբ մետաղադրամը վայրէջք կատարի, այն կա՛մ գրվածքի կողմով կլինի, կա՛մ պատկերի: Այնուամենայնիվ, քվանտային աշխարհում, քանի դեռ մետաղադրամն օդում է (մինչ վայրէջք կատարելը և մեր դիտելը), այն գտնվում է այսպես ասած «սուպերպոզիցիոն» վիճակում, որտեղ այն և՛ գրվածքի կողմով է, և՛ պատկերի: Չափումը կամ դիտումը քվանտային վիճակի մասին տեղեկություն ստանալու միակ միջոցն է: Միայն չափումից (դիտումից) հետո է մետաղադրամը «ընտրում» հնարավոր վիճակներից մեկը: 

Այժմ փորձենք առավել հստակ ներկայացնել քվանտային սուպերպոզիցիայի գաղափարը: Դիցուք՝ ալիքային ֆունկցիայի Ψ1 վիճակում դիտարկումը հանգեցրել է մի արդյունքի. օրինակ՝ զառն ընկել է 1 թվի վրա, իսկ Ψ2 վիճակում՝ 2 թվի վրա: Այդ դեպքում կարելի է պնդել, որ Ψ1և Ψ2-ի ցանկացած գծային կոմբինացիա (օրինակ՝ aΨ1 + bΨ2 տեսքի ֆունկցիան, որտեղ a-ն և b-ն հաստատուններ են) նկարագրում է ալիքային ֆունկցիայի մի վիճակ, որի ժամանակ նույն դիտարկումը ևս հանգեցնում է վերը նշված արդյունքներից որևէ մեկին: Քվանտային համակարգի վիճակները նկարագրող ալիքային հավասարումների համախումբը (այսինքն՝ զառի ընկնելու բոլոր հնարավոր վիճակները) նշանակենք Ψn: Կստացվի, որ համակարգի կամայական պահի վիճակը նկարագրող ալիքային հավասարումը` Ψ-ն, Ψn ֆունկցիաների ինչ-որ գծային կոմբինացիա է՝ Ψ = Σ anΨn, որտեղ an –երը հաստատուններ են, որոնց քառակուսիները նկարագրում են տվյալ վիճակում հայտնվելու հավանականությունը: Այս բանաձևը հնարավորություն է տալիս չափումների միջոցով որոշելու քվանտային համակարգի այս կամ այն վիճակի դիտարկման հավանականությունը: Ընդ որում, այդ հավանականությունների, այն է՝ an հաստատունների քառակուսիների գումարը հավասար է 1-ին` ալիքային ֆունկցիայի կոլապսից հետո համակարգը կհայտնվի հնարավոր Ψn վիճակներից որևէ մեկում, իսկ մնացած վիճակները մեր դիտարկման համար հանգած արդյունքներ կդառնան: Հենց սա է քվանտային սուպերպոզիցիայի գաղափարը (տե՛ս նկ. 2):

Այժմ խոսենք մի գիտնականի մասին, որի կատուն, գուցե, ավելի հայտնի է, քան հենց ինքը՝ գիտնականը: Խոսքն Էրվին Շրյոդինգերի մասին է: Նա առաջ է բերել հետևյալ պարադոքսը․ պատկերացրե՛ք մի տուփ, որի մեջ փակված են մի կատու և մի մեխանիզմ, որը կարող է սպանել կատվին: Այն ակտիվանում է ատոմի ռադիոակտիվ քայքայման արդյունքում, ինչի հավանականությունը 50/50 է: Ըստ քվանտային մեխանիկայի, քանի դեռ տուփը փակ է, և համակարգը չի դիտարկվում, ատոմը գտնվում է «տրոհված» և «չտրոհված» վիճակների սուպերպոզիցիայի մեջ։ Հետևաբար՝ նաև կատուն է գտնվում կենդանի/մեռած սուպերպոզիցիոն վիճակում: Այս փորձը ցույց է տալիս սուպերպոզիցիայի սկզբունքը՝ մինչև դիտարկման պահը մի քանի միմյանց բացառող վիճակների միաժամանակյա գոյության հնարավորությունը։ Կատվի ճակատագրի մասին հետաքրքրվողներին շտապենք հանգստացնել, քանի որ իրական կյանքում այս փորձը Շրյոդինգերը չի կատարել: Նա նույնիսկ կատու չի ունեցել:

Քվանտային համակարգերի այս սկզբունքն օգտագործվում է քվանտային ալգորիթմներում, ինչպիսին է, օրինակ, Գրովերի ալգորիթմը տվյալների բազայի որոնման համար։ Նմանատիպ ալգորիթմները հնարավորություն են տալիս լուծելու որոշակի խնդիրներ շատ ավելի արագ, քան դասական ալգորիթմները՝ շնորհիվ բազմաթիվ հնարավոր լուծումներ միաժամանակ մշակելու ունակության։

Սուպերպոզիցիան նոր վիճակների մեխանիկական «ավելացում» չէ: Սուպերպոզիցիայի յուրաքանչյուր վիճակ ունի իր հավանականության լայնույթը, որն ազդում է չափման արդյունքում համակարգը հենց այդ վիճակում հայտնաբերելու հավանականության վրա: Ընդ որում՝ լայնույթները կարող են խանգարել կամ օգնել միմյանց՝ ուժեղացնելով կամ թուլացնելով որոշակի արդյունքի հավանականությունը, ինչը քվանտային հաշվարկի ևս մեկ հզոր կողմ է:

Հայզենբերգի անորոշությունը

1927 թվականին գիտնական Վերներ Հայզենբերգը ներկայացրեց մի աներևակայելի կոնցեպտ, որն ընդմիշտ փոխեց ֆիզիկայի աշխարհը: Խոսքն անորոշության սկզբունքի մասին է: Հայզենբերգի սկզբունքը պնդում է, որ անհնար է միաժամանակ չափել մասնիկի դիրքն ու իմպուլսը բացարձակ ճշտությամբ։ Պարզ ասած, եթե փորձեք մեծ ճշտությամբ չափել մասնիկի դիրքը, ապա անխուսափելիորեն կխախտեք նրա իմպուլսը, և հակառակը։

Այստեղ մենք կրկին հանդիպում ենք միկրո և մակրո աշխարհների հիմնական տարբերությանը: Դասական աշխարհում մարմնի դիրքն ու արագությունը չափելիս մենք նրա վրա որևէ կերպ չենք ներգործում, և իդեալական տարբերակում մենք կարողանում ենք միաժամանակ չափել օբյեկտի և՛ արագությունը, և՛ կոորդինատները բացարձակ ճշտությամբ (այլ կերպ ասած՝ զրոյական անորոշությամբ):

Քվանտային աշխարհում, սակայն, ցանկացած չափում ազդում է համակարգի վրա: Հենց այն փաստը, որ մենք չափում ենք, օրինակ, մասնիկի դիրքը, հանգեցնում է նրա արագության փոփոխության, ընդ որում՝ անկանխատեսելի: Եվ եթե մեզ հաջողվի զրոյական սխալանքով (բացարձակ ճշգրիտ) որոշել չափվող մեծություններից որևէ մեկը, ապա մյուս մեծության անորոշությունը կհասնի անվերջության, և մենք ոչինչ չենք իմանա դրա մասին։ Սակայն շատ կարևոր է հասկանալ, որ Հայզենբերգի անորոշության սկզբունքը որևէ կերպ չի ենթադրում, որ մասնիկի բնութագրիչներից որևէ մեկը՝ տարածական դիրքը կամ արագությունը, հնարավոր չէ չափել անհրաժեշտ ճշտությամբ (տե՛ս նկ. 3):

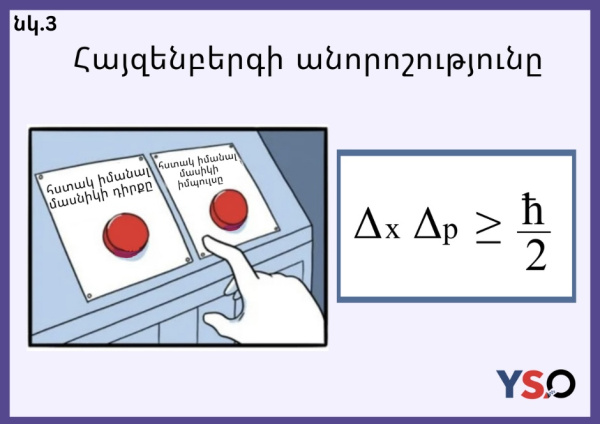
Իրականում անորոշության սկզբունքը կապում է ոչ միայն տարածական կոորդինատներն ու արագությունը: Պարզապես այս օրինակի վրա այն առավել հեշտ է բացատրել: Նմանատիպ դատողությունների միջոցով մենք գալիս ենք այն եզրահանգման, որ անհնար է ճշգրիտ չափել քվանտային համակարգի էներգիան և որոշել ժամանակի այն պահը, երբ այն ունի այդ էներգիան:

Հայզենբերգի անորոշության սկզբունքը ժամանակին մի շարք վիճաբանությունների առիթ դարձավ, սակայն այժմ այն ժամանակակից ֆիզիկայի անբաժան մասն է կազմում:

Շրյոդինգերի հավասարումը

Պատկերացրե՛ք m զանգվածով մասնիկ, որը շարժվում է x առանցքի երկայնքով որևէ ուժի ազդեցությամբ։ Դասական մեխանիկայում օգտվելով Նյուտոնի երկրորդ օրենքից՝ կարող ենք որոշել մասնիկի դիրքը ցանկացած պահի, և այդ դիրքը որոշակի է։ Մենք կարող ենք պարզել  մասնիկի արագությունը, իմպուլսը, կինետիկ էներգիան և այլն: Քվանտային մեխանիկայում մենք փնտրում ենք մասնիկի ալիքային ֆունկցիան, որը կարող ենք ստանալ՝ լուծելով Շրյոդինգերի հավասարումը։ Շրյոդինգերի հավասարումը Նյուտոնի երկրորդ օրենքի տրամաբանորեն անալոգային դերն է կատարում։ Հաշվի առնելով սկզբնական պայմանները`  Շրյոդինգերի հավասարումը (տե՛ս նկ. 4) տալիս է ալիքային ֆունկցիան հաջորդ պահերի համար ճիշտ այնպես, ինչպես դասական մեխանիկայում Նյուտոնի օրենքը որոշում է  մարմնի կոորդինատը ապագա ժամանակների համար: 

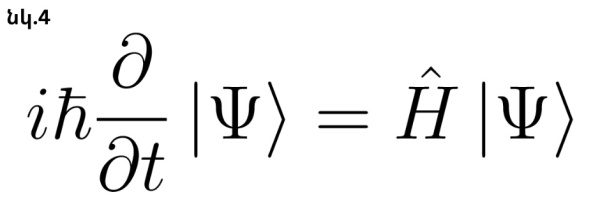
Քվանտային մեխանիկայի ժամանակակից խնդիրները

Եթե միայն իմանաք, թե գիտնականների միջև ինչքան վեճեր են ծագել քվանտային երևույթներն ուսումնասիրելիս...

Մակրո և միկրոաշխարհների միջև տարբերությունը այսօր արդեն որևէ ապացույցի կարիք չունի: Շատ փորձերի միջոցով արդեն հաստատվել է, որ քվանտային տեսությունը ճիշտ է, բայց ամեն դեպքում դասական ֆիզիկայի հետ տարաձայնությունները շատ են: Այժմ կխոսենք դրանցից մի քանիսի մասին:

1.   Քվանտային մեխանիկայի և հարաբերականության ընդհանուր տեսության անհամատեղելիությունը

Քվանտային մեխանիկան նկարագրում է մատերիայի և էներգիայի վարքը փոքր մասշտաբներում, իսկ հարաբերականության ընդհանուր տեսությունը նկարագրում է գրավիտացիան տիեզերական մասշտաբներում: Այս երկու տեսությունները համատեղելի չեն, այդ պատճառով մինչ այսօր գիտնականներին չի հաջողվում մշակել գրավիտացիայի քվանտային տեսություն: Եթե ճիշտ է քվանտային մեխանիկան, ապա հարաբերականության ընդհանուր տեսությունը սխալ է, և հակառակը: Այն փորձերը, որոնք հաջողվել է կատարել, ապացուցել են քվանտային տեսության ճշմարտացիությունը: Իսկ օրինակ՝ գրավիտացիոն ալիքները գրավիտացիոն տեսության փորձնական ապացույց են:

2. Դիտողի դերը

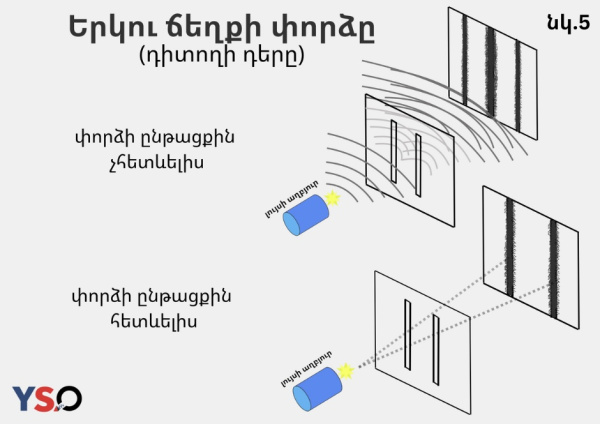
Մեզ համար ամեն դեպքում անհասկանալի է՝ ով է «ընտրում», թե ինչու համակարգը հնարավոր վիճակներից հենց այդ մեկում պետք է գտնվի, ինչից է կախված այդ «ընտրությունը»: Չէ՞ որ ալիքային հավասարումը ցույց է տալիս միայն համակարգի հաջորդ վիճակում գտնվելու հավանականության խտությունը, բայց այն ոչ մի կերպ չի բացառում, որ հաջորդ վայրկյանին համակարգը կգտնվի ավելի քիչ հավանական վիճակում: Դասական ֆիզիկայում մեզ երբեք չի հետաքրքրել դիտողի ազդեցությունը համակարգի պահվածքի վրա: Առանց դիտողի մասնակցության էլ արևը կծագի և մայր կմտնի, գնդակը թեք հարթության վրայով կսահի: Ամեն դեպքում քվանտային աշխարհում այդպես չէ, և լրիվ անտեսել դիտողի աղդեցությունը համակարգի վիճակի ընտրության հարցում սխալ կլինի (տե՛ս նկ. 5):

3. Քվանտային խճճվածություն

Այս երևույթը ի հայտ է գալիս այն ժամանակ, երբ քվանտային մասնիկները իրար հետ այնքան մոտ են փոխազդում, որ նրանց քվանտային վիճակը հնարավոր չէ այլևս տարանջատել: Իրարից հեռանալուց հետո նրանց կապված կարգավիճակը պահպանվում է՝ չնայած նրանց միջև ֆիզիկական հեռավորությանը: Այս երևույթի հիմքում ընկած ենթադրությունը ժամանակին Էյնշտեյնին «չափից շատ էր դուր եկել»: Ամենազարմանալին այն է, որ մի մասնիկի վիճակի փոփոխությունը ակնթարթորեն հանգեցնում է մյուսի վիճակի փոփոխությանը, և հավանաբար այդ վիճակների փոփոխման արագությունը գերազանցում է լույսի արագությանը: Այս ենթադրությունը թուլացնում է դասական ֆիզիկայի հիմքերը, քանի որ դրանք հիմնված են լույսի արագության անգերազանցելիության վրա: Ի հակադրություն քվանտային խճճվածության երևույթի՝ գիտնականներ Էյնշտեյնը, Պադոլսկին և Ռոզենը առաջ են քաշել հետևյալ պարադոքսը: Դրա հիմքում այն գաղափարն է, որ քվանտային խճճվածության երևույթի արդյունքում մասնիկները այլևս չեն կարող նկարագրվել իրարից անկախ: Հետևաբար, եթե մենք իմանանք մի մասնիկի կոորդինատները, միանգամից կարող ենք իմանալ մյուսինը՝ անկախ նրանց միջև եղած հեռավորության: Ապա չափելով մի մասնիկի իմպուլսը՝ կարող ենք միանգամից իմանալ մյուսինը: Գաղափարը հակասում էր մերձազդեցության տեսությանը, ըստ որի, մարմինների միջև փոխազդեցությունները չեն կարող տեղի ունենալ ակնթարթորեն. փոխազդեցության արագությունը չի կարող ավելի մեծ լինել, քան լույսի արագությունը: Բայց ինչպես տեսանք, քվանտային խճճվածության երևույթի հիմքում հակառակ գաղափարն է․ այն, կարելի է ասել, հեռազդեցության տեսության օրինակ է: Էյնշտեյնը պարադոքսն օգտագործում էր քվանտային տեսության ոչ լիարժեքությունը ցույց տալու համար՝ նշելով, որ քվանտային խճճվածության գաղափարը միայն ավելի թերի է դարձնում այն: Իսկ ժամանակի մյուս ամենահայտնի գիտնական Նիլս Բորը հեռազդեցության գաղափարը համարում էր քվանտային տեսության ամենակարևոր առանձնահատկությունը:

Վերջապես 2022 թ. Նոբելյան մրցանակի արժանացան ֆիզիկոսներ Ջոն Կլաուզերը, Ալեն Ասպեն և Անտոն Ցայլինգերը, որոնք, բացի նրանից, որ կարողացել են փորձնականորեն ապացուցել քվանտային խճճվածության գաղափարը, նաև հիմք են դրել քվանտային տեխնոլոգիաների զարգացմանը:

4.   Քվանտային մեխանիկայի ինտերպրետացիաները

Քվանտային մակարդակում տեղի ունեցող երևույթների մեկնաբանությունը այսօր էլ ֆիզիկոսների շրջանում ակտիվ քննարկումների առարկա է: Քվանտային մեխանիկայի ինտերպրետացիաները բազմազան են: Դրանցից յուրաքանչյուրը յուրովի է մեկնաբանում քվանտային պրոցեսները:

Չնայած այս բոլոր խնդիրներին՝ քվանտային տեսությունը ամեն դեպքում շատ լավ կարողանում է մեկնաբանել տարբեր երևույթներ: Տեսությունը պարզապես լրացման կարիք ունի: 

Հոդվածը պատրաստեցին ԵՊՀ ֆիզիկայի ինստիտուտին առընթեր գործող օպտիկների միջազգային կազմակերպության ուսանողական մասնաճյուղի («YSO Student Chapter») ներկայացուցիչները